
Найти площадь треугольника
Данный сервис поможет вам найти площадь треугольника онлайн.
Треугольник – геометрическая фигура, образованная тремя точками, не лежащими на одной прямой, и соединёнными между собой. Длина каждой стороны треугольника не превосходит суммы длин двух других сторон.
В любом треугольнике сумма углов равна 180° или π радиан. Также в любом треугольнике против равных сторон лежат равные углы, а против большей стороны лежит больший угол.
Площадь треугольника можно найти по разным формулам.
Если известна хотя бы одна из сторон и высота, опущенная на это сторону, то площадь находится как половина произведения этих величин:
Формула площади треугольника по известной стороне и высоте
Если известна хотя бы одна из сторон и высота, опущенная на это сторону, то площадь находится как половина произведения этих величин:
$$S = {1\over 2} \cdot a \cdot h_a = {1\over 2} \cdot b \cdot h_b = {1\over 2} \cdot c \cdot h_c.$$Если известны две стороны и угол между ними, то площадь треугольника можно найти, умножив эти величины и разделив на 2:
$$S = {1\over 2} \cdot a \cdot b \cdot \sin(C) = {1\over 2} \cdot a \cdot c \cdot \sin(B)={1\over 2}\cdot b \cdot c \cdot \sin(A)$$В данном онлайн-сервисе используется формула Герона для вычисления площади треугольника (необходимо знать длины трех сторон):
$$S=\sqrt{p \cdot (p-a) \cdot (p-b) \cdot (p-c)} $$где
$$p={a+b+c \over 2}$$
- Найти площадь треугольника с длинами сторон 5, 7 и 10
Посмотреть решениеДано:
$$a = 5 \quad b = 7 \quad c = 10 $$
Решение:По формуле Герона:
$$S=\sqrt{p \cdot (p-a) \cdot (p-b) \cdot (p-c)} $$ , где
$$p={a+b+c \over 2}$$ – полупериметр.
$$p= {(5 + 7 + 10)\over 2} = 11$$
Следовательно $$S=\sqrt{11 \cdot (11-5) \cdot (11-7) \cdot (11-10)} = 16,24808$$
Ответ:
$$S=16,24808$$
- Найти площадь треугольника с длинами сторон 6, 7 и периметром 22
Посмотреть решениеДано:
$$a = 6 \quad b = 7 \quad P = 22$$
Решение:Предварительно вычислим полупериметр и длину третьей стороны:
$$p={P \over 2} = 11$$ – полупериметр$$c = P - a - b = 22 - 6 - 7 = 9$$
Теперь воспользуемся формулой Герона:$$S=\sqrt{p \cdot (p-a) \cdot (p-b) \cdot (p-c)} $$
$$S=\sqrt{11 \cdot (11-6) \cdot (11-7) \cdot (11-9)} = 20,97618 $$
Ответ:
$$S = 20,97618$$
- Три окружности с радиусами 6, 7, 8 внешне попарно касаются друг друга. Найти площадь треугольника, образованного центрами этих окружностей.
Посмотреть решение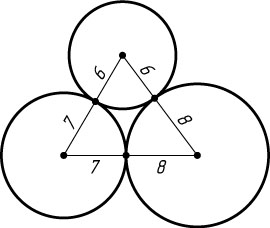
Дано:
$$r_1 = 6 \quad r_2 = 7 \quad r_3 = 8$$
Решение:Отрезки, соединяющие центры двух касающихся окружностей, проходят через точку их касания, следовательно длины сторон треугольника, образованного центрами этих окружностей,
будут равны 13, 14, 15.$$р = {(13 + 14 + 15) \over 2} = 21$$ – полупериметр
а площадь по формуле Герона:$$S=\sqrt{p \cdot (p-a) \cdot (p-b) \cdot (p-c)} $$
$$S=\sqrt{21 \cdot (21-13) \cdot (21-14) \cdot (21-15)} = 84$$
Ответ:
$$S = 84$$
-
Найти площадь равнобедренного прямоугольного треугольника с гипотенузой длиной 5.
Посмотреть решениеДано:
$$a = b \quad c = 10$$
Решение:Используя теорему Пифагора, находим длины катетов треугольника:
$$a^2 + b^2 = c^2$$
$$a^2 + a^2 = 10^2$$
$$2a^2 = 100$$
$$a = \sqrt50 = 7,071$$
Теперь вычисляем полупериметр: $$p = {(a + b + c) \over 2}$$
и подставляем полученные значения в формулу Герона:
$$S = \sqrt{(р \cdot (р - a) \cdot (р - b) \cdot (р - c))} = 24.99952 = 25$$
Ответ:
$$S = 25$$
- Найти площадь равностороннего треугольника с периметром 30.
Посмотреть решениеДано:
$$a = b = c$$
$$P = 30$$
Решение:
Предварительно вычислим длины трех сторон и полупериметр:$$a = b = c = P / 3 = 10$$
$$p = {P \over 2} = 15$$
Теперь воспользуемся формулой Герона:
$$S = \sqrt{(15 · (15 - 10) · (15 - 10) · (15 - 10))} = \sqrt{1875} = 43.30127$$
Ответ:
$$S = 43.30127$$

