
Найти площадь ромба
Ромб – особый вид параллелограмма, у которого все стороны равны, а противоположные углы тоже равны.
Диагонали ромба перпендикулярны друг другу, также они являются осями симметрии ромба.
Диагонали делят углы пополам, так как они являются и биссектрисами углов. В ромб можно вписать окружность.

Площадь ромба можно найти по нескольким формулам.
Если известны стороны и острый угол, то площадь ромба находится как произведение квадрата стороны на синус угла:
$$S = a^2 \cdot \sin(A)$$Если известны стороны ромба и высота, опущенная на одну из сторон, то площадь можно найти, перемножив эти величины:
$$S = a \cdot h$$Данный сервис использует формулу расчёта площади ромба, если известны диагонали:
$$S = {d_1 \cdot d_2 \over 2}$$
- Найти площадь ромба с диагоналями 10 и 6.
Посмотреть решениеДано:
$$d_1 = 10$$
$$d_2 = 6$$
$$\pi = 3.14$$
Решение:$$S = {(d_1 \cdot d_2) \over 2} = 10 \cdot {6 \over 2} = 30$$
Ответ:
$$S=30$$
- Найти площадь ромба ABCD, если известно, что радиусы описанных около треугольников ABD и ABC окружностей равны 10 и 20, соответственно.
Посмотреть решение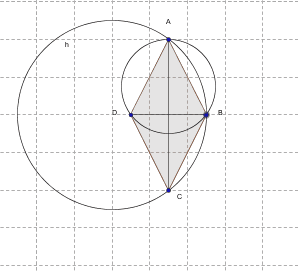
Дано:
$$R = 20$$
$$r = 10$$
Решение:Обозначим $$\angle BAC = \widehat A$$.
Тогда
$$AB = 2 \cdot R \cdot \sin \angle ACB = 2 \cdot R \cdot \sin \widehat A, AB = 2 \cdot r \cdot \sin \angle BDA = 2 \cdot r \cdot \sin(90° - \widehat A) = 2 \cdot r \cdot \cos \widehat A$$
следовательно, $$\tan \widehat A = {r \over R} = {1 \over 2}$$
Отсюда $$\widehat A = \arctan \left({1 \over 2} \right) = 0.4636476$$
Теперь можно вычислить длины диагоналей ромба:
$$AC = 2 \cdot R \cdot \sin (2 \cdot \widehat A) = 40 \cdot 0.8 = 32$$,
$$BD = 2 \cdot r \cdot \sin (2 \cdot \widehat A) = 20 \cdot 0.8 = 16$$.
Значит площадь ромба будет равна:
$$S = {1 \over 2} \cdot d_1 \cdot d_2 = {1 \over 2} \cdot 32 \cdot 16 = 256$$
Ответ:
$$S = 256$$
- Найти площадь ромба со стороной 5 и диагональю 8
Посмотреть решение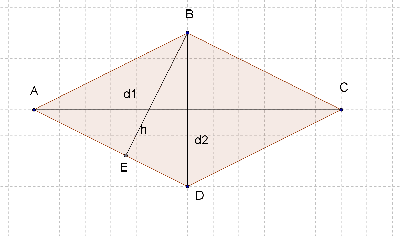
Дано:
$$a = 5$$
$$d_1 = 8$$
Решение:По теореме Пифагора:
$$a^2 = \left({d_1 \over 2} \right)^2 + \left({d_2 \over 2}\right)^2$$ , т.е.$$5^2 = \left( {8 \over 2} \right)^2 + ({d_2 \over 2})^2$$, откуда
$$\left({d_2 \over 2}\right)^2 = 9$$, значит
$${d_2 \over 2} = 3 $$
Следовательно площадь ромба будет равна:
$$S = {1 \over 2} \cdot d_1 \cdot d_2 = 24 $$
Ответ:
$$S = 24$$
-
Найти площадь ромба с длиной высоты 3, если его высота, опущенная на основание, делит его пополам.
Посмотреть решение
Дано:
$$h = 3$$
$$|AE| = |ED|$$
Решение:Пусть а - длина стороны ромба, а d1 и d2 - длины его диагоналей, тогда по теореме Пифагора получаем:
$$а^2 = \left({а \over 2} \right)^2 + h^2$$ и
$$d_2^2 = \left({а \over 2} \right)^2 + h^2$$
Следовательно: $${3 \over 4} \cdot а^2 = 32$$, значит
$$а^2 = 12$$, откуда
$$d_2^2 = 12$$
Снова, воспользовавшись теоремой Пифагора получаем:
$$а^2 = \left( {d_1 \over 2} \right)^2 + \left( {d_2 \over 2} \right)^2$$ , отсюда
$$\left({d_1 \over 2} \right)^2 = {3 \over 4} \cdot а^2 = 3^2 =9$$, следовательно:
$$d_1= {\sqrt 36} = 6$$ и
$$d_2= {\sqrt 12} = 3,4641$$
Следовательно площадь ромба будет равна:
$$S = {1 \over 2} \cdot d1 \cdot d2 = 10,3923$$
Ответ:
$$S = 10,3923$$
- Найти площадь ромба с периметром 40 и углом между сторонами 60°.
Посмотреть решениеДано:
$$Р = 40$$
$$ \angle ab = 60^o$$
Решение:
Так как длины всех сторон в ромбе равны, то длина одной стороны будет равна:
$$a = {P \over 4} = 10.$$
Так как диагонали ромба одновременно являются его биссектрисами и делятся точкой пересечения пополам, то, обозначив длины диагоналей через $$d_1$$ и $$d_2$$, получаем:
$$d_1 = 2 \cdot 10 \cdot \sin 30°$$ и $$d_2 = 2 \cdot 10 \cdot \cos 30 ^\circ$$, откуда:
$$d_1 = 10, d_2 = 17,32 $$
Следовательно площадь ромба будет равна:
$$S = {1 \over 2} \cdot d_1 \cdot d_2 = 86,6$$
Ответ:
$$S = 86,6$$
